Classification
01 Background
What is classification? Take a unlabeled test case, a dimensional input (a vector of features), and assign it to one of discrete (in most cases) classes . When , it is denoted as binary classification, and when , it is multi-class classification.
What are key classification algorithms?
- Logistic Regression
- Softmax Regression
- Support Vector Machines
- Decision Trees
- K-Nearest Neighbor
- Bayesian Classifier
- Classification Ensemble
- Bagging, AdaBoost, Stacking, Cascading, Random Forest
What are common classification tasks?
- Spam vs Not Spam Email Classification
- ImageNet Image Classification
Multi-label Classification
02 Core Concepts
What is Precision, Recall, and Accuracy?
What is True Positive, True Negative, False Positive, False Negative? Positive and Negative simply represent two different outcomes. For example, Spam/Not Spam for Emails. Let’s set Spam to be Positive, Not Spam to be Negative.
- TP would mean “correctly identifying email as Spam when the email is indeed Spam”.
- FP would mean “incorrectly identifying email as Spam when the email is indeed Not Spam” (misclassifies a legitimate email)
- TN would mean “correctly identifying email as Not Spam when the email is indeed Not Spam”
- FN would mean “incorrectly identifying email as Not Spam when the email is indeed Spam” (fails to identify spam)
Accuracy:
Problems solved by Precision
Precision measures the proportion of the correctly predicted positive instances out of all instances predicted as positive. In the Spam/Not Spam example, the number of emails that were actually spam out of the ones predicted to be spam. This also expresses the proportion of instances that were predicted to be relevant that are actually relevant. It focuses on the cost of FP. A major downside, however, does not consider FN, it does not account for cases where we fail and miss positive instances. This can be balanced with the Recall
Recall Aka True Positive Rate, Sensitivity: measures the proportion of.correctly predicted instances out of all instances that are actually positive. In the Spam/Not Spam example, it would measure, of those that were actual spam, what proportion of those were accurately classified as spam. This is also known as the ability to get all relevant instances.
What is F1 Score (Harmonic Mean), Precision vs Recall? A ML metric that assess the predictive skill of a model by elaborating on it’s class-wise performance rather than an overall performance as done by accuracy (which is reliable only when each class of dataset has same number of samples). It combines precision and recall. The formula is
Why? There is often a tradeoff between precision and recall. Higher precision means answers must be more correct. This can be as a result of (1) an increase in TP, perhaps from developing a better model. (2) a decrease in False Positives, perhaps developing tools that isolate edges cases. For example, in Spam/Not Spam example, our model can learn to become more strict / more confident about classifying an email as a spam. Precision increases because you only classify emails as spam when you are really sure that it is spam. In this case, recall decreases because you may even doubt emails that might be spam as not spam.
High recall gives all the right answers, but garbage as well. You can get high recall from (1). For example, in the Spam/Not Spam example, you lower the standard and classify more emails as spam.
More Examples
- Filtering Spam/Not Spam
- Summary: High Precision may be better because users may not want to miss an important email (spam emails put into spam folder) because of a misclassified spam message. Users can flag an email as spam if need to.
- Screening for Cancer/Non Cancer
- High Recall: Rescreening individuals who have a 30% chance of cancer
- High Precision: Rescreening individuals who have a 90% chance of cancer
- Summary: High Recall may be better because it is better to find all patients that possibly have cancer (for further testing or screening) than simply getting patients who are more likely to have cancer. It would be dangerous to miss a person with cancer.
The harmonic mean is used over a simple average because it punishes extreme values.
Thus, it important to understand what your goal is, higher precision, or higher recall. But, in some cases, F1 may simply be a better estimation of performance than just using either or.
What is the ROC Curve and AUC? Short for Receiver Operating Characteristic. It plots the TPR true positive rate against FPR false positive rate (Fall Out, False Alerts). The FPR is the proportion of negative cases incorrectly defined as positive.
In the Spam Not Spam example, FPR answers the question of what fraction of non-spam will be classified as spam
Here is a ROC graph.
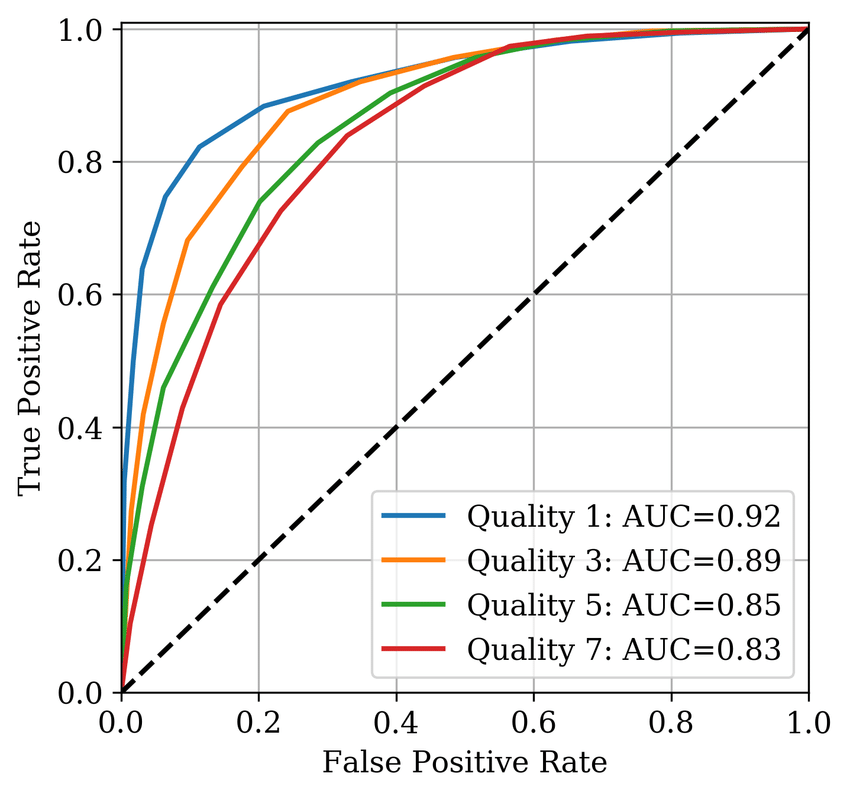 This graph makes it possible to see how the trade-off between a model’s sensitivity and specificity is represented by plotting TPR vs FPR at various threshold settings. It AUC area under the curve, and is used as a metric to asses a classifiers general performance. An AUC of 1 would represent perfect. If it is close to 0.5 it is regarded as a bad classifier. More specifically
This graph makes it possible to see how the trade-off between a model’s sensitivity and specificity is represented by plotting TPR vs FPR at various threshold settings. It AUC area under the curve, and is used as a metric to asses a classifiers general performance. An AUC of 1 would represent perfect. If it is close to 0.5 it is regarded as a bad classifier. More specifically
- Big AUC → High Precision (low FPR ) and recall (High TPR )
- Low AUC → Low Precision (high FPR) and recall (Low TPR)
Let’s also define Specificity (TNR) as We can see that FPR is . Some graphs may label as instead of FPR.
In the Spam Not Spam example, Specificity, answers the question of what fraction non-spam that the spam filter finds. Low FPR means high specificity.
Accuracy and Evaluation Metrics
- Jaccard Index
- Log Loss
Multi-class Classification with Softmax
In a multi-class classification task. The last layer is dimensional vector, where is the number of classes. The last layer should contain probabilities that an input is of a each class. These probabilities should add to one.
For example, recognizing cats, dogs, baby chicks and others. The last layer should contain something like. where is the input.
Thus, we apply the softmax activation function to the . The softmax activation function is Element wise exponentiation. So this produces a vector. t = e^{\left( z^{(L)} \right)} \tag{1} The output is a^{[L]} = \frac{e^{z^{[L]}}}{\sum_{j=1}^{4}t_{j}}\tag{2} Normalized to the sum of one, which also gives a vector. An example is shown below. z^{[L]} = \begin{bmatrix} 5 \\ 2 \\ -1 \\3 \end{bmatrix}, \space t= \begin{bmatrix} e^{5} \\ e^{2} \\ e^{-1} \\ e^3 \end{bmatrix}\tag {3} Tips
- When no hidden layers, can make linear decision boundaries.
- Called “soft max” in contrast to “hard max”
- If , soft-max reduces to logistic regression.
Loss function is Categorical Cross Entropy
Multi-label Classification with Sigmoid
Also known is independent logistic classifiers. For example sigmoid classifier.